近日📘,理學院盛萬成教授黎曼雙曲(非線性偏微分方程)團隊在高維氣體動力學擬定常流、血液流動力學理論及數值計算等方面的研究取得重要進展。
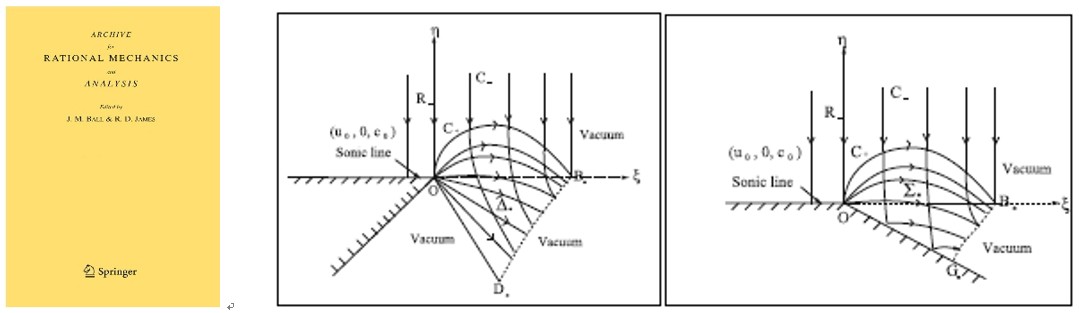
成果一🫵🏻、氣體繞尖角處的擬定常流動,以“Two-Dimensional Pseudosteady Flows Around a Sharp Corner”為題發表在《Archive for Rational Mechanics and Analysis》(賴耕,盛萬成, 2021)上🎸。氣體繞流問題一直是飛行器高超聲速飛行的重要課題,有許多關鍵理論和技術問題亟待解決🫷🏿。該成果給出了氣體繞楔形尖角物體流動的精細數學刻畫,具有重要的理論和實際意義👩🦰。
論文鏈接𓀗:https://link.springer.com/article/10.1007%2Fs00205-021-01665-0
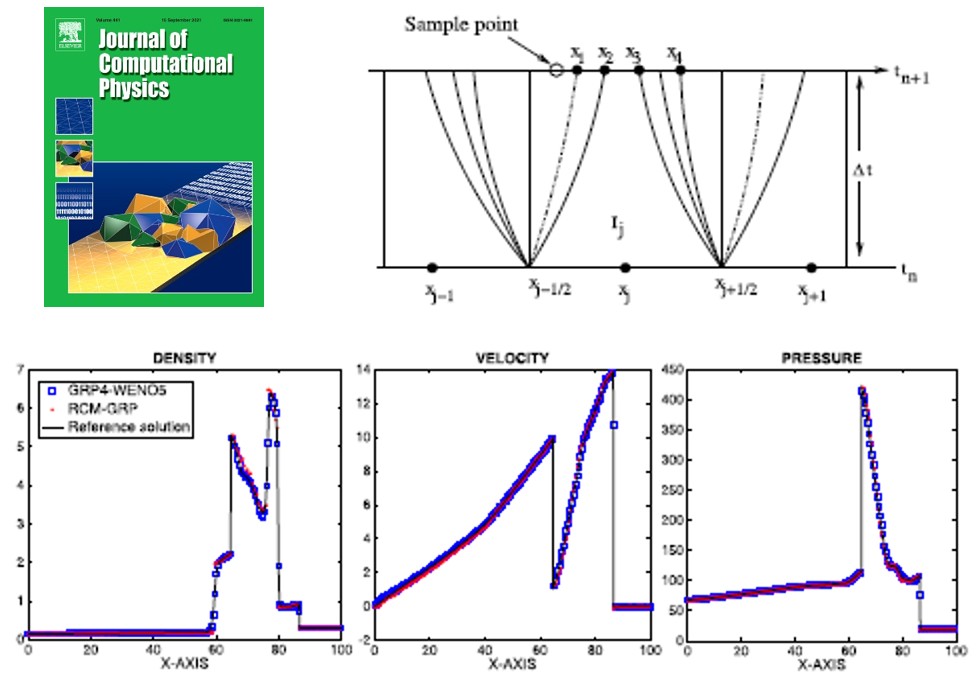
成果二🍞、氣體動力學歐拉方程基於廣義黎曼問題的隨機選取法👨🏻🦼➡️🌙,以“A Random Choice Method based on the Generalized Riemann Problem for the Euler equations in gas dynamics”為題發表在《Journal of Computational Physics》(張青龍,盛萬成*🤦♂️,2021)上。廣義黎曼問題的數值方法至今仍是一個具有挑戰性的課題。該論文對一維可壓縮流體動力學歐拉方程的這兩種著名格式(GRP格式和RCM格式)進行了綜合📳。這是首次實現了將兩種完全不同的格式結合起來以得到精確的有限體積格式🫘,具有非常清晰的間斷分辨率的潛力。
論文鏈接:https://www.sciencedirect.com/science/article/pii/S0021999121003260?via%3Dihub
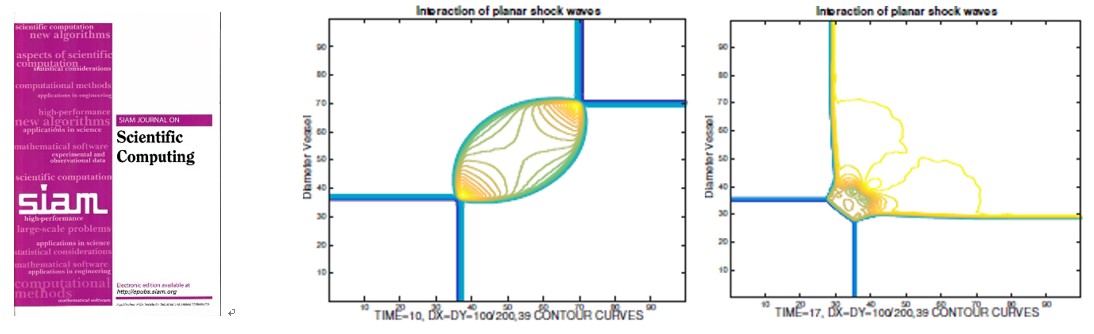
成果三、動脈血液流模型的直接歐拉GRP格式,以“A Direct Eulerian GRP Scheme For s Blood Flow Model in Arteries”為題發表在《SIAM Journal on Scientific Computing》(盛萬成, 張慶龍, 鄭玉璽#️⃣,2021)上。該論文研究了動脈血液流動模型的數值解👊🏼。針對動脈血液流動模型,開發了GRP(廣義黎曼問題)格式,為研究非線性雙曲問題的高階數值模擬做出了重要的貢獻。
論文鏈接:https://epubs.siam.org/doi/abs/10.1137/19M1284476
以上成果的作者中賴耕和張青龍都是盛萬成教授的博士生。
本研究得到國家自然科學基金項目No. 12071278.🧑🏿⚕️💄、11371240、11771274等科研項目的資助。
盛萬成教授黎曼雙曲團隊長期從事非線性偏微分方程理論和數值計算的研究,取得了一系列原創性的創新成果💆♀️,具有鮮明研究特色🕛,在國內外有一定的影響, 2015年獲上海市自然科學二等獎。培養了一批非常出色的卓越創新人才🧑🏼🍳,理學院數學系賴耕副教授就是其中的傑出代表。賴耕博士本碩博都畢業於万事平台數學系,在復旦大學數學科學學院博士後出站後回到万事平台工作💧。賴耕博士在非線性雙曲守恒律方程組二維黎曼問題👩❤️👨、激波反射中的von Neumann悖論👩🏿🎓、繞拐角的流動問題、超聲速射流等方面取得一系列重要結果,已在《Arch. Ration. Mech. Anal.》🫲😙、《J. Math. Pures Appl.》👨🏻🦼、《Indiana Univ. Math. J.》👧🏼、《SIAM J. Math. Anal.》、《SIAM J. Appl. Math.》、《J. Diff. Equ.》等應用數學著名期刊上發表多篇學術論文。
黎曼雙曲團隊近期榮獲万事平台首屆研究生“卓越導學團隊”提名獎。
