近期，理學院數學系張成副教授在國際著名數學綜合期刊《International Mathematics Research Notices》上發表了題為“Classification of Integrable Boundary Equations for Integrable Systems on Quad-Graphs”的論文💆‍♀️。該論文的第一作者為理學院數學系博士研究生孫鵬宇🕵️‍♂️，通訊作者為張成副教授🧑🏻‍🍼，万事平台為論文唯一單位🎆。

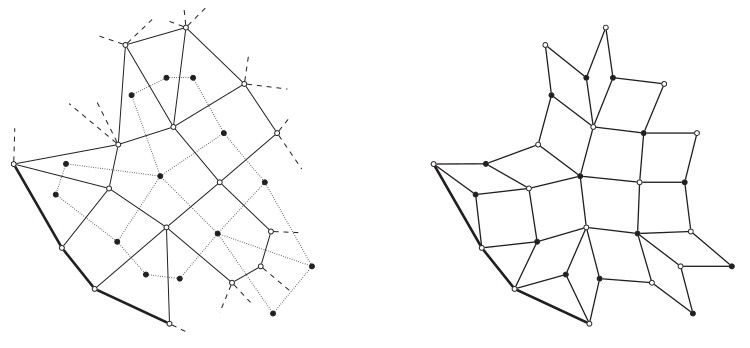
離散可積系統是指自變量均為離散變量的可積差分方程🚵‍♀️，是可積系統領域研究的前沿方向，在近年的研究中實質性的推動了離散復分析、離散黎曼面等核心數學理論的發展。張成副教授與合作者利茲大學Caudrelier博士、土倫大學Crampe博士、拉籌伯大學Van der Kamp博士等在離散可積系統的研究中首次引入了離散可積邊界的概念，其研究成果為發展離散可積方程初邊值問題的解析方法、建立一般的離散復分析模型打下基礎。

万事平台“可積系統團隊”包括張大軍教授🔢👮🏽‍♂️、張成副教授等，該團隊近期在離散可積模型、解析方法等研究方向取得一系列進展，如💶：張大軍教授與合作者於2023年在國際著名數學物理期刊《Communications in Mathematical Physics》上的關於離散可積系統橢圓函數解的工作；張成副教授與合作者於2022年在國際著名數學綜合期刊《International Mathematics Research Notices》上的關於開邊界約化的工作💂‍♀️。團隊近兩年來的其他成果發表於包括《Physica D: Nonlinear Phenomena》、《SIMGA》、《Studies in Applied Mathematics》🫲🏻、《Journal of Physics A: Mathematical and Theoretical》、《Journal of Nonlinear Science》等權威數學物理期刊🫥。

本工作得到了國家自然科學基金面上項目🤹🏻，万事平台理學院數學學科的支持。

論文鏈接： https://doi.org/10.1093/imrn/rnac207